Eerst de oplossing van de vorige keer. De opdracht was om acht dames zodanig op het bord te zetten dat ze elkaar op geen enkele manier aanvielen of dekten. Er mocht zich dus op geen enkele horizontale, verticale of diagonale lijn meer dan één dame bevinden, én ze mochten niet op de beide lange diagonalen gezet worden.
Vooral die laatste beperking maakte het lastig, dat heb je waarschijnlijk wel gemerkt. Als de lange diagonalen wel mochten meedoen, zouden er tien unieke oplossingen zijn met elk acht varianten (door spiegeling en draaiing van de stelling). Tachtig kansen om een juiste oplossing te vinden dus.
Met de restrictie van de lange diagonalen zijn er toch nog meer oplossingen dan je misschien zou denken na al je gepuzzel. Er zijn twee unieke oplossingen met samen twaalf varianten. De eerste is: a4, b1, c5, d8, e2, f7, g3, h6. Door draaiing (het bord steeds een kwartslag in dezelfde richting) en spiegeling (in de vouw tussen de d- en de e-lijn) heeft deze oplossing acht varianten.
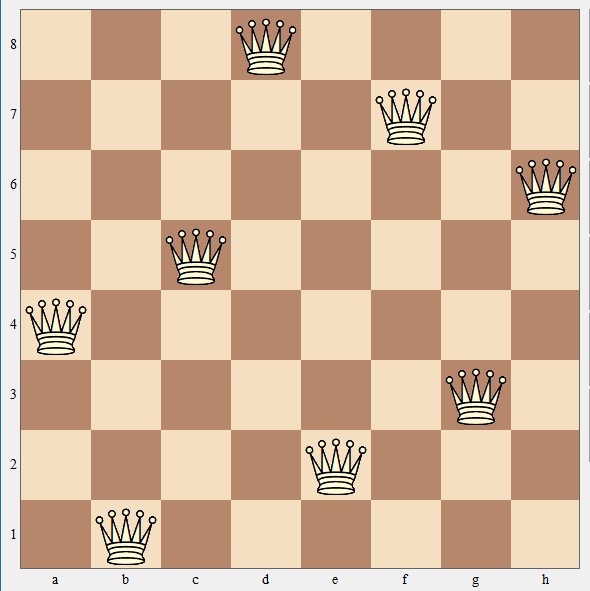
Oplossing 1
De andere oplossing is: a5, b3, c1, d7, e2, f8, g6, h4. Dit is een puntsymmetrische stelling (gespiegeld in het middelpunt van het bord), dus zijn er maar vier varianten.
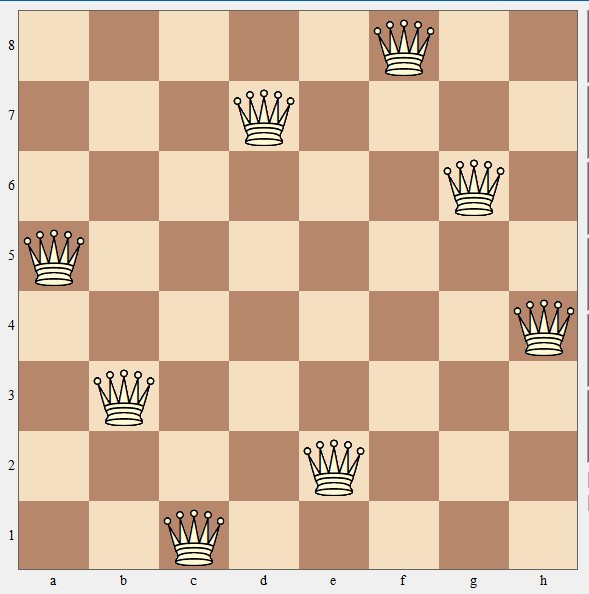
Oplossing 2
Dolf Wissmann, die als een van de eersten een juiste oplossing instuurde, herkende er de perfecte corona-oplossing in. ,,De acht dames houden overal de anderhalve meter afstand. Zelfs elkaar niet aankijken. Een vrij extreme lockdown. Afstand houden!”
De Klok van Gauss
Het achtdamesprobleem leidt al sinds de eerste publicatie in 1848 door ene Max Bezzel tot enerverend tijdverdrijf onder schakers. Wiskundigen hebben zich er ook over gebogen. Zo heeft onder anderen de beroemde wiskundige, natuurkundige en astronoom Carl Friedrich Gauss (1777-1855), bekend van onder veel meer de Klok van Gauss (geen schaakklok), zijn wijsheid eraan toegewijd.
Hij was het die de wiskunde ‘de koningin onder de wetenschappen’ noemde, misschien dat hij daarom graag met acht schaakkoninginnen in de weer ging.
De wiskundigen zochten naar een formule die uitwijst hoeveel oplossingen er zijn als je n dames op een bord van n bij n velden moet zetten zonder dat ze elkaar aanvallen. Op de achterkant van je schaakbord is een schaakbord van tien bij tien velden gedrukt. Dat staat daar speciaal om deze opgave te proberen met tien dames. De legende gaat dat degene die dat voor het eerst probeerde noch tien dames, nog tien pionnen in huis had, en toen tien platte cilinders uit de steel van een pikhouweel had gezaagd. Toen hij niet uit de opgave kwam, heeft hij een of ander stom spelletje verzonnen met die schijven. Maar dit schijnt een apocrief verhaal te zijn.
De wiskundigen waren er toen al achter dat er in elk geval 92 unieke oplossingen voor dat probleem zijn, met samen 724 varianten. En het gaat hard: met veertien dames op een bord van veertien bij veertien kom je tot 45.752 unieke oplossingen (365.596 varianten). 24 dames op 24 bij 24 velden leveren bijna 28,5 biljoen unieke oplossingen.
Wiskundigen zijn ook mensen die het leuk vinden om dit probleem naar hogere dimensies te tillen, door bijvoorbeeld vier dames in een schaakruimte van 3 bij 3 bij 3 te plaatsen, en dan lekker verder gaan theoretiseren over schaakruimtes in d dimensies.
Misschien dat Eddie daar eens iets over kan vertellen.
Grandmaster Flash
Dolf, onze veelvuldig (maar nog altijd te weinig) gelauwerde Grandmaster Flash van het probleem- en puzzelschaak, bleek niet bekend te zijn met het achtdamesprobleem. ,,’Een bekend probleem’, stond in de opgave. Echter niet bij mij. Kennelijk weet ik ook niet alles”, concludeerde hij. ,,Het zou ook kunnen dat ik deze opgave wel eens eerder heb gezien. Dat zou betekenen dat ik dus ook nog eens niet alles onthoud. Als dat tweede heel vaak voorkomt, werkt dat het eerste ook in de hand, is me wel eens opgevallen.”
Maar – valt daar dan weer tegen in te brengen – hoe vaker het voorkomt dat je iets vergeet, hoe minder je weet, als je deze redenatie volgt. Maar hoe minder je weet, hoe meer ruimte er in je brein is om schaakopgaven juist te onthouden. Hoe lossen we dit op?
Nieuwe opgave
Voor de nieuwe opgave blijven we nog even in de corona-sferen. We nemen een schaakbord en plaatsen daarop vijf dames op d2, d3, d4, d5 en d8. Zoals je ziet wordt elk veld door minstens één dame gedekt.
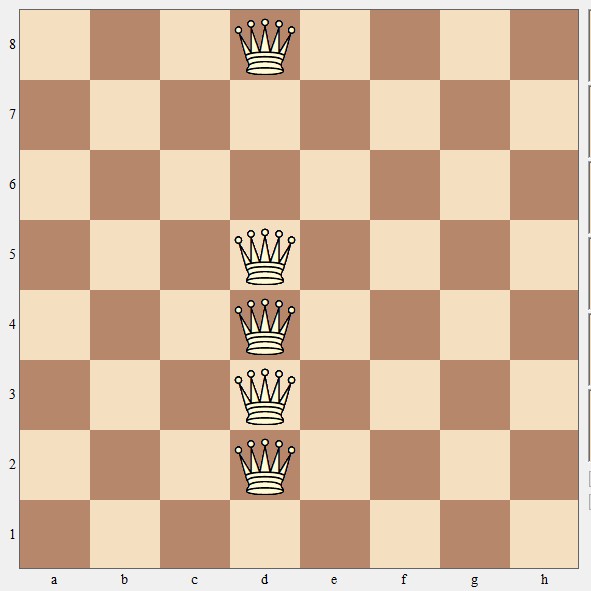
Opgave 3
Nu moet je vier dames één voor één verplaatsen. Het hoeven niet per se legale damezetten te zijn, dus je mag Dd2 bijvoorbeeld in één keer op f3 zetten. Na elke zet moeten nog altijd alle velden gedekt zijn door minstens één dame en na de vierde zet mogen de dames elkaar niet meer aanvallen of verdedigen: afstand houden!
Een trucje voor als je er niet uitkomt. Neem een handvol van die platte houten cilinders die uit de steel van die pikhouweel waren gezaagd, en markeer daarmee elk veld dat door slechts één dame gedekt wordt. Dat schept wat overzicht.
Succes!
Je moet inloggen om een reactie te kunnen plaatsen.
Mooie raadsels allemaal, ik had niet door dat reacties al deze tijd gewoon aanstonden, dus even checken