Het oudste bekende schaakraadsel is meer dan vijfhonderd jaar oud! Het is het Probleem van Guarini en stamt uit 1512, lees ik in Wiskunde op een schaakbord van John J. Watkins. Het gaat om vier paarden, twee witte en twee zwarte, op een schaakbordje van drie bij drie velden. We gebruiken dus alleen de linkeronderhoek van ons bord: de negen velden tussen a1, a3, c3 en c1. De witte paarden staan op a1 en c1 en de zwarte op a3 en c3.
De opgave is nu om de witte en de zwarte paarden van plaats te laten ruilen door alleen maar legale paardzetten uit te voeren, waarbij er natuurlijk nooit twee stukken op hetzelfde veld mogen staan. De vraag is: in hoeveel zetten kan dat?
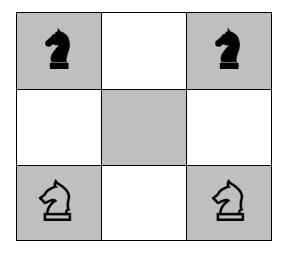
Fig. 1. Laat de paarden met legale paardzetten verwisselen van plaats. In hoeveel zetten kan dat?
Probeer het nu eerst zelf voor je verder leest, want de oplossing geef ik straks meteen voordat ik het eigenlijke raadsel van deze week opgeef. Om te voorkomen dat je stiekem naar beneden kijkt, komt nu eerst de oplossing van vorige week.
Torusschaakbord
We speelden op een torusschaakbord, een bord zonder randen dus. Er stond een zwarte koning op e8, een witte koning op e2, een witte dame op f5 en een wit paard op b5. Wit moest mat geven in vier zetten.
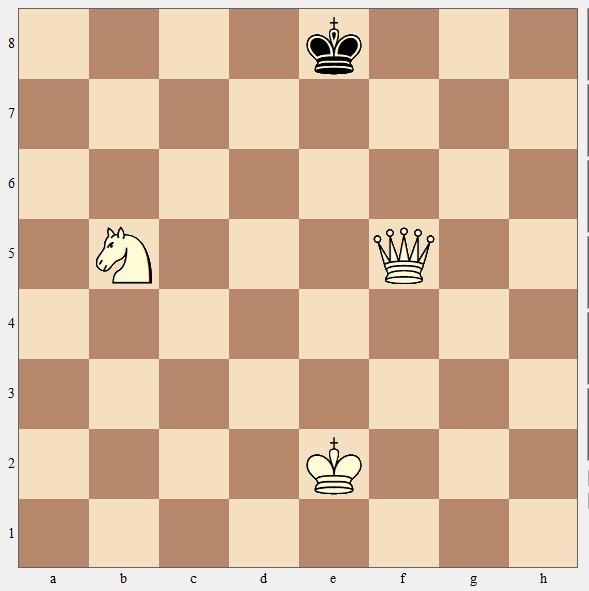
DIAGRAM VAN DE VORIGE OPGAVE
Je zult gezien hebben dat de zwarte koning niet ‘over de rand’ naar de andere kant van het bord mag vluchten, want dan krijg je hem nooit in vier zetten te pakken. De witte koning houdt hem nu dus mooi op afstand. Nu moet de dame ervoor zorgen dat de zwarte koning ook niet naar het midden van het bord kan vluchten, anders red je het ook niet op tijd. Dus: 1. Dh7 en dan heeft zwart maar twee zetten:
Deze keer was er maar één inzending, die gelukkig correct was. Dolf had er een tijdje over gedaan, zei hij. ,,Ik was al enige tijd bezig toen ik me ineens herinnerde dat het soms best clever kan zijn als je slim bent.”
Dolf schoof de vier stukken twee velden naar omlaag, zodat er minder randoverschrijdend spel nodig was en toen zag hij de oplossing snel. Hij zag nóg iets moois toen hij de beide matstanden met elkaar vergeleek. ,,Hetzelfde fraaie matbeeld, maar gespiegeld en de vier stukken – zeg maar – één veldje lager op het bord.”
Terug naar Guarini
Dan de oplossing van het Probleem van Guarini. Toch nog lastiger dan het lijkt op zo’n klein bordje hè. Waar het om gaat is dat je het probleem moet ontdoen van lastige bijzaken. In de eerste plaats de lastige structuur van de paardzet in combinatie met de geometrie van het bord, steeds één veld recht en één veld schuin. Maak daar eens rechte lijnen van. Als je alle velden waar de paarden langskomen met een lijnstuk verbindt, zie je een achtpuntige ster ontstaan, oftewel een octagram: a1-c2-a3-b1-c3-a2-c1-b3 en terug naar a1. Veld b2 blijft onaangeroerd, daar kan geen paard komen.

Figuur 2. De paardensprongen zijn met rechte lijnen weergegeven.
Nu gaan we ook de bordstructuur loslaten. Trek als het ware de ster uit elkaar tot een regelmatige achthoek, ook wel een octagon genoemd. Ineens zie je het: de paarden lopen gewoon een rondje achter elkaar aan! Ombeurten doen ze elk vier stappen in dezelfde richting, tegen de klok in of met de klok mee, totdat ze van plaats verwisseld zijn.
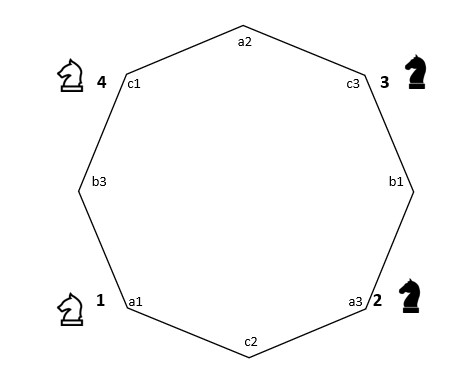
Fig. 3. De paardenrondgang is uit elkaar getrokken en vormt nu een octagon. De oplossing is meteen duidelijk.
Nu moeten we dat nog even terugvertalen naar het schaakbord, maar dat is niet moeilijk meer.
Nu heeft elk paard een stap gezet en gaan we verder.
Voilà: Pa1 is in vier stappen op c3 uitgekomen, Pc1 op a3, Pa3 op c1 en Pc3 op a1. De oplossing is: zestien zetten.
Je hebt nu met mathematische abstractie een complex probleem ontdaan van verwarrende details die een helder zicht op de oplossing belemmeren. Eerst de paardensprong weergegeven als een rechte lijn, en toen het schaakbord uit elkaar getrokken. Je hebt het schaakraadsel teruggebracht tot een diagram, tot een verzameling punten (‘knopen’ genoemd), waarvan sommige volgens een bepaalde logica met elkaar verbonden zijn met lijnen (‘randen’ of ‘kanten’). Dat heet een graaf.
In de wiskunde is men gek op dit soort vereenvoudiging. Het is zelfs een complete deelwetenschap: de grafentheorie.
De wiskundige Leonhard Euler (1707-1783) verrichtte veel denkwerk op dit gebied. Hij boog zich over de ‘wandeling’ of ‘rondgang’ langs de knopen van een graaf, waarbij elke knoop precies één keer wordt aangedaan: een eulerwandeling of eulerrondgang. Hij wilde het ook helemaal perfect doen en aan het slot terugkeren bij de eerste knoop. Dan is er sprake van een eulercykel.
Euler deed dit onder andere met een paard op een schaakbord. Eén paard springt met 64 paardensprongen over het bord, waarbij het precies één keer op elk veld komt en terugkeert op het beginveld. Probeer zelf deze eulercykel maar eens te vinden.
De opgave
Dan de opgave van deze keer. We gebruiken een schaakbordje van drie bij vier velden, dus het deel van het bord tussen a1, a4, c4 en c1. Er staan witte paarden op a1, b1 en c1, en zwarte op a3, b3 en c3.

Figuur 4.
De opgave is om met legale paardzetten de drie witte paarden van positie te laten verwisselen met de drie zwarte. De vraag is: wat is het minimumaantal zetten dat je daarvoor nodig hebt? De oplossing is weer te vinden via de grafentheorie, dus eerst de eulerrondgang op het bordje vinden en uittekenen, en dan het bord uit elkaar trekken. De vorm ziet er dan natuurlijk anders uit dan bij het 3×3-bord.