De vorige keer hadden we drie witte paarden en drie zwarte paarden op een schaakbordje van drie bij vier velden, zeg maar het deel van het bord tussen de velden a1, a4, c4 en c1. De drie witte paarden stonden op de onderste rij, de drie zwarte op de vierde rij. Ze moesten met legale zetten van plaats wisselen, en de vraag was hoeveel zetten je daar minimaal voor nodig had.
Er was opnieuw maar één oplossing. Dolf Wissmann had zich over de opgave gebogen. Daar was hij even mee bezig. “Jij praat er makkelijk over, over vinden, uittekenen en uit elkaar trekken, maar ik heb hier een bord en ik heb stukken, mijn knutselset ben ik hier al decennia lang niet meer tegengekomen”, grapte hij. Hij ging het proberen met ‘gewoon schaken’.
Met zijn eerste poging was hij wel “een paar uurtjes” zoet. Dit deed mij definitief concluderen dat de gegeven opgave te moeilijk moet zijn geweest. Dolf is op deze plaats al eerder de Grandmaster Flash van het probleem- en puzzelschaak genoemd, en daarmee is geen woord te veel gezegd. Als hij al een paar uur bezig is met één opgave…
Hij kwam tot een oplossing van – zoals dat heet in het onder probleemschakers gebruikelijke jargon – 9,0 zetten, dus negen zetten van wit en negen van zwart. Dat wil zeggen: als wit en zwart ombeurten een zet doen. Dat is in partij- en probleemschaak een voorwaarde, maar bij raadselschaak hoeft dat niet. Dan mag hetzelfde paard twee zetten achter elkaar doen.
Dan kan het sneller, maar ook weer niet heel veel sneller. Het thema van de opgave was de grafentheorie uit de wiskunde. We moesten dus eerst een paardenrondgang over alle velden maken en de paardensprongen weergeven in rechte lijnen.

.Merk op dat de velden een nummer hebben gekregen en dat je de rondgang niet op elk veld kunt beginnen.
De tweede stap was dat we de structuur van het schaakbord moesten vergeten door er een graaf van te maken.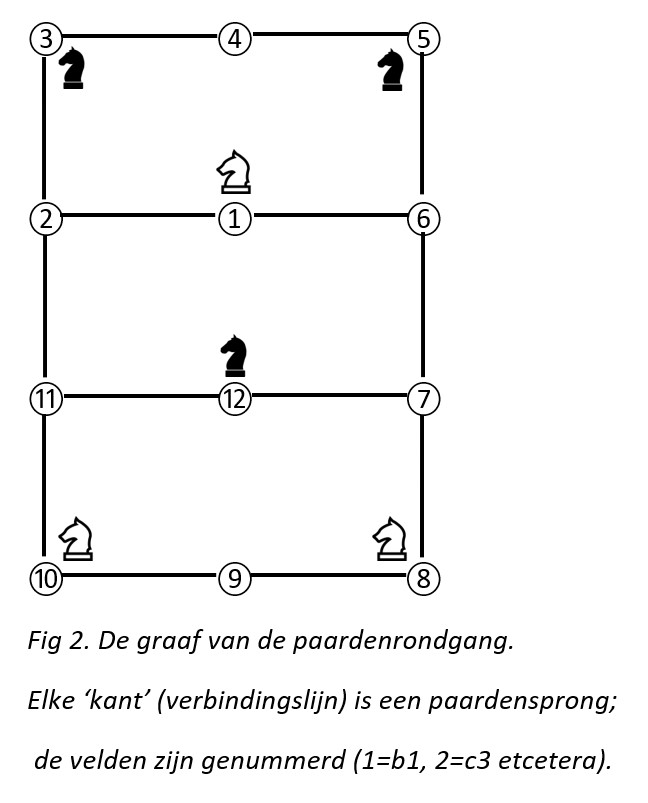
.Nu is de oplossing makkelijker te vinden. We zien we dat er zeven zetten nodig zijn om de drie zwarte stukken naar hun gewenste posities te brengen. Het paard van knoop 5 gaat drie stappen recht omlaag naar knoop 8. Eén paard loopt in twee sprongen van 3 naar 1 en één paard maakt ook twee sprongen van 12 naar 10.
Het complete stel verplaatsen in veertien zetten (zeven voor elke kleur) lukt helaas niet, want er staat steeds één keer een paard van de andere kleur in de weg. Eén paard zal op enig moment moeten plaatsmaken.
We hoeven het nu alleen nog maar te vertalen naar paardzetten op het schaakbordje.
Er zijn dus minimaal zestien zetten nodig, slechts twee minder dan Dolf had gevonden met de officiële zetvolgorde.
Maar goed, dit was dus een te moeilijke opgave. Jammer van die prachtige wiskunde die jullie nu allemaal mislopen. Ik was namelijk van plan een raadsel op te geven waarbij op een möbius-bord geschaakt moest worden, een rondlopend bord met maar één zijde, zodat de stukken ook aan de ‘achterkant’ van ons bekende bord ondersteboven geplakt kunnen zitten!
En als jullie dat onder de knie zouden hebben gekregen, zou ik verder gaan met schaken op een kleinfles, dus twee aan elkaar genaaide möbiusbanden zodat er een fles ontstaat waarbij de binnenkant tegelijk te buitenkant is!
En dan had ik jullie vertelt dat jullie de leukste wiskundeprofessor op YouTube kunnen zien vertellen over zijn verzameling kleinflessen (zoek maar op: Clifford Stoll heeft een aantal superleuke vlogs op het kanaal Numberphile).
Maar we doen het dus voor de nieuwe opgave met een gewoon bord en gewone stukken. Dat wil zeggen: bíjna gewoon, want we hebben vier dames nodig.
De opdracht is: plaats vier dames en één paard zodanig op het schaakbord dat alle velden gedekt of bezet zijn. Als je er niet uit komt: ietsjes simpeler is het met vier dames en een loper.
Succes!